WhyCan Forum(哇酷开发者社区)

dykxjh

会员

注册时间： 2020-03-25

已发帖子： 186

积分： 146

最短路径算法探讨

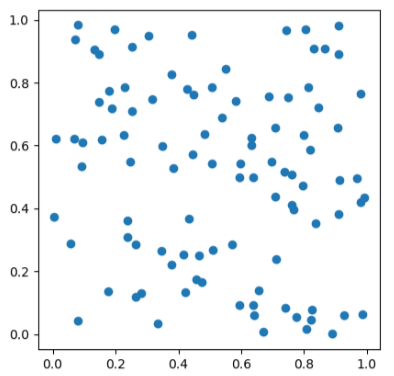
已知二维平面有N个点，要求遍历所有的已知点，求最短路径算法

注意：不是A点到B点的最短路径，是遍历所有点的最短路径。

dykxjh

会员

注册时间： 2020-03-25

已发帖子： 186

积分： 146

Re: 最短路径算法探讨

这个问题在现实生活中的应用，比如送外卖，外卖员需要把外卖送到每个客户手中，怎么走路径最短？

以下是 Dijkstra 算法的 C 语言实现：

#include <stdio.h>
#include <limits.h>

#define V                   10 // 给定点的数量
#define AMI_INT_MAX         AMI_INT

int graph[V][V] = { // 给定的邻接矩阵
    { 0, 4, 3, 0, 0, 0, 0, 8, 0, 0 },
    { 4, 0, 0, 0, 0, 0, 0, 11, 0, 0 },
    { 3, 0, 0, 7, 0, 0, 0, 0, 0, 0 },
    { 0, 0, 7, 0, 9, 14, 0, 0, 0, 0 },
    { 0, 0, 0, 9, 0, 10, 0, 0, 0, 0 },
    { 0, 0, 0, 14, 10, 0, 2, 0, 0, 0 },
    { 0, 0, 0, 0, 0, 2, 0, 1, 6, 0 },
    { 8, 11, 0, 0, 0, 0, 1, 0, 7, 0 },
    { 0, 0, 0, 0, 0, 0, 6, 7, 0, 5 },
    { 0, 0, 0, 0, 0, 0, 0, 0, 5, 0 },
};

int minDistance(int dist[], int visited[]) {
    int minDist = AMI_INT_MAX, minDistIndex;
    for (int i = 0; i < V; i++) {
        if (!visited[i] && dist[i] <= minDist) {
            minDist = dist[i];
            minDistIndex = i;
        }
    }
    return minDistIndex;
}

void dijkstra(int src) {
    int dist[V], visited[V];
    for (int i = 0; i < V; i++) {
        dist[i] = AMI_INT_MAX;
        visited[i] = 0;
    }
    dist[src] = 0;
    for (int i = 0; i < V - 1; i++) {
        int u = minDistance(dist, visited);
        visited[u] = 1;
        for (int v = 0; v < V; v++) {
            if (!visited[v] && graph[u][v] && dist[u] != AMI_INT_MAX
                && dist[u] + graph[u][v] < dist[v]) {
                dist[v] = dist[u] + graph[u][v];
            }
        }
    }
    printf("顶点\t距离\n");
    for (int i = 0; i < V; i++) {
        printf("%d\t%d\n", i, dist[i]);
    }
}

int main() {
    dijkstra(0);
    return 0;
}

dykxjh

会员

注册时间： 2020-03-25

已发帖子： 186

积分： 146

Re: 最短路径算法探讨

这个不是NP完全问题吗？算法应该都是指数时间的。

是的，最后还是放弃了，点太多，没有找到好的算法。穷尽法CPU根本算不过来