WhyCan Forum(哇酷开发者社区)

打老虎

会员

注册时间： 2019-04-03

已发帖子： 16

积分： 36

研究了下Tslib内关于触摸屏校准的算法，水一贴

最近搞个触摸屏校准，参考了Tslib，感觉这个算法挺巧妙，为了不让自己半天计算白费，

借晕哥宝地怒水一贴，数学算法可能大伙不感兴趣，就当随笔了，本人数学渣，

若有不当处高手请轻拍。

一般触摸屏校准无非以下几种情况：

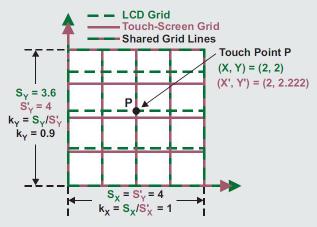
          图1 比例

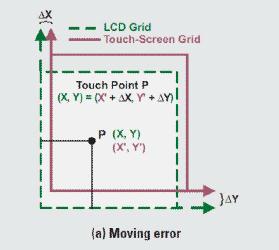
           图2 移动

 
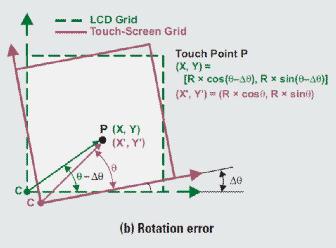
           图3 旋转

根据触摸的AD值和LCD分辨率不同，两者会有比例关系。触摸屏安装的时候可能会和LCD不太契合，
比如贴歪了，可能会有移动和旋转的误差，使得两者坐标有偏差。

正因为有这些误差，才需要校正。假设屏上有个P点，在LCD的坐标是(X, Y)，在触摸屏上是(X', Y')。
在二维坐标下上面三种情况分别可以用如下三个矩阵表示（不是我编的）：

咱也不用考虑当前哪种情况了，假设三个误差都存在（某项不存在的话，后面带入计算自然会去除掉），就全部乘一下：

其中 X，Y是LCD坐标由自己设定，X′和Y′触摸屏的坐标，由测量得知。
而我们目的就是求αx，βx，ΔX和αy，βy，ΔY这6个未知数而已，那只要构建6个方程，
只需要取屏幕上3个点即可。

注意：重点来了不要被上面的推导过程吓到，又是三角函数又是矩阵相乘，
其实没人会关心触摸屏和LCD到底贴歪了多少度，移动了多少个像素点，
只要知道我们的目的是为了求这些系数，这些值能帮助我们将触摸屏坐标转化为LCD坐标就可以了，
更简化且平易近人的写法如下：

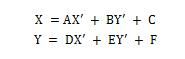
解方程的话，可以用克拉默法则，自己玩的话随便取3个点手算也行，注意3点法需要取独立点，
即在屏幕上画出三个已知LCD坐标的点，最好不要连成一条线，然后记录下这些点的触摸屏坐标，
代入方程可得：

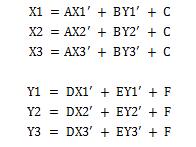
这样可以求出A，B，C，D，E和F，若按矩阵写法(还是换回α和β的写法)如下：

写成方程就是 b= A∙x，或x = A-1 ∙ b，其中A是系数矩阵，b是常数列向量，x是未知数列向量。
对应上面x坐标的公式b就是: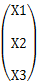
，

未知数列向量就是:
。

注：要求的线性方程x = A-1 ∙ b中，A-1=A*/|A|，设Δ = |A|也就是系数矩阵A的行列式值，
伴随矩阵A*与b相乘之后得到Aj，那么未知数解xj = |Aj|/|A|。
本方程3个未知数的|A1|，|A2|和|A3|标记为为Δx1、Δx2和Δx3，
那么3个未知数解分别是αx = Δx1/Δ，βx = Δx2/Δ，ΔX = Δx3/Δ。这是克拉默法则。

以上铺垫完毕，通通不用记住，下面说说Tslib里面的5点法，或者叫n点法，改写上面的矩阵如下：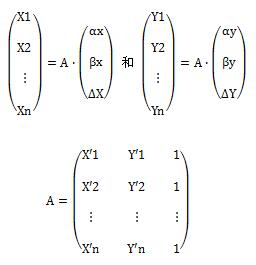

按照之前3点法的解法我们也用克拉默法则，但是忽然发现A居然不是方阵！！
A是nx3（n>3）的矩阵！A-1都没有意义了！x = A-1 ∙ b都没了！

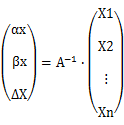
和

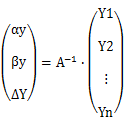
还有啥用！！

等等，有点大惊小怪了，不是方阵的话A-1就是个伪逆矩阵吧！n>3左逆矩阵为 A-1 = (ATA)-1 AT，
那么公式变为:
           

为啥要这么变？别和我说什么最小二乘解左逆右逆什么最优解之类的，我就是想要搞个方阵，
A的转置AT 和A相乘就变成方阵，令A = ATA，b = ，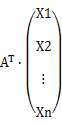

这样x = A-1 ∙ b又来了！接下来只要求出ATA和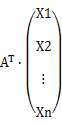就可以用克拉默法则了。

         

为了计算方便我们定义如下：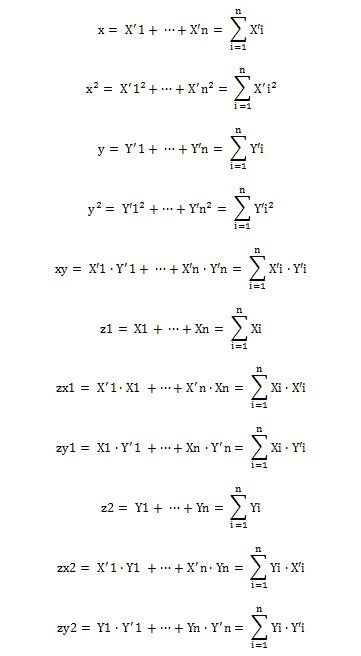

那么可以放心求解：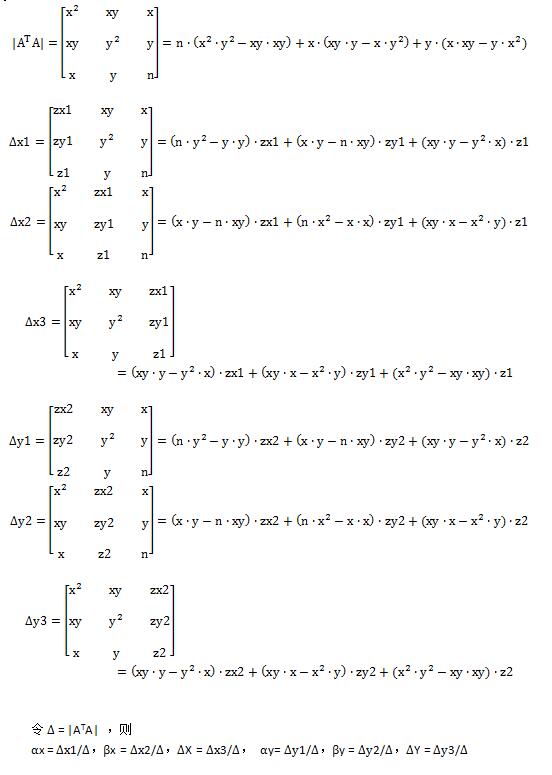

令Δ = |ATA| ，则
αx = Δx1/Δ，βx = Δx2/Δ，ΔX = Δx3/Δ， αy= Δy1/Δ，βy = Δy2/Δ，ΔY = Δy3/Δ

重点来了，以上公式统统不用纠结，带入上面公式可以发现一个规律：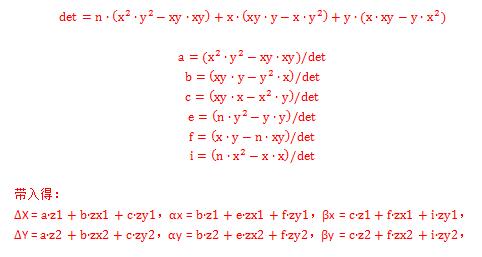

此时会发现这些红色的系数公式和Tslib内的perform_calibration函数内的一模一样。完结撒花。

附：

/*
 *  tslib/tests/ts_calibrate_common.c
 *
 *  Copyright (C) 2001 Russell King.
 *
 * This file is placed under the GPL.  Please see the file
 * COPYING for more details.
 *
 * SPDX-License-Identifier: GPL-2.0+
 *
 *
 * common functions for calibration
 */
#include <stdio.h>
#include "ts_calibrate.h"

int perform_calibration(calibration *cal)
{
	int j;
	float n, x, y, x2, y2, xy, z, zx, zy;
	float det, a, b, c, e, f, i;
	float scaling = 65536.0;

	/* Get sums for matrix */
	n = x = y = x2 = y2 = xy = 0;
	for (j = 0; j < 5; j++) {
		n += 1.0;
		x += (float)cal->x[j];
		y += (float)cal->y[j];
		x2 += (float)(cal->x[j]*cal->x[j]);
		y2 += (float)(cal->y[j]*cal->y[j]);
		xy += (float)(cal->x[j]*cal->y[j]);
	}

	/* Get determinant of matrix -- check if determinant is too small */
	det = n*(x2*y2 - xy*xy) + x*(xy*y - x*y2) + y*(x*xy - y*x2);
	if (det < 0.1 && det > -0.1) {
		printf("ts_calibrate: determinant is too small -- %f\n", det);
		return 0;
	}

	/* Get elements of inverse matrix */
	a = (x2*y2 - xy*xy)/det;
	b = (xy*y - x*y2)/det;
	c = (x*xy - y*x2)/det;
	e = (n*y2 - y*y)/det;
	f = (x*y - n*xy)/det;
	i = (n*x2 - x*x)/det;

	/* Get sums for x calibration */
	z = zx = zy = 0;
	for (j = 0; j < 5; j++) {
		z += (float)cal->xfb[j];
		zx += (float)(cal->xfb[j]*cal->x[j]);
		zy += (float)(cal->xfb[j]*cal->y[j]);
	}

	/* Now multiply out to get the calibration for framebuffer x coord */
	cal->a[0] = (int)((a*z + b*zx + c*zy)*(scaling));
	cal->a[1] = (int)((b*z + e*zx + f*zy)*(scaling));
	cal->a[2] = (int)((c*z + f*zx + i*zy)*(scaling));

	printf("%f %f %f\n", (a*z + b*zx + c*zy),
			     (b*z + e*zx + f*zy),
			     (c*z + f*zx + i*zy));

	/* Get sums for y calibration */
	z = zx = zy = 0;
	for (j = 0; j < 5; j++) {
		z += (float)cal->yfb[j];
		zx += (float)(cal->yfb[j]*cal->x[j]);
		zy += (float)(cal->yfb[j]*cal->y[j]);
	}

	/* Now multiply out to get the calibration for framebuffer y coord */
	cal->a[3] = (int)((a*z + b*zx + c*zy)*(scaling));
	cal->a[4] = (int)((b*z + e*zx + f*zy)*(scaling));
	cal->a[5] = (int)((c*z + f*zx + i*zy)*(scaling));

	printf("%f %f %f\n", (a*z + b*zx + c*zy),
			     (b*z + e*zx + f*zy),
			     (c*z + f*zx + i*zy));

	/* If we got here, we're OK, so assign scaling to a[6] and return */
	cal->a[6] = (int)scaling;

	return 1;
}

参考资料：
Calibration in touch-screen systems.pdf

最近编辑记录 打老虎 (2020-03-08 23:03:40)

打老虎

会员

注册时间： 2019-04-03

已发帖子： 16

积分： 36

Re: 研究了下Tslib内关于触摸屏校准的算法，水一贴

太深奥了，看不懂，前排帮顶

haha,多谢多谢

只是研究了下Tslib里校准算法的原理，看了TI一篇文档，用数学推导了下，发现两者结果是一样(就是结尾红字部分)。

打老虎

会员

注册时间： 2019-04-03

已发帖子： 16

积分： 36

Re: 研究了下Tslib内关于触摸屏校准的算法，水一贴

感谢楼主分享，所有字我都认识

打老虎

会员

注册时间： 2019-04-03

已发帖子： 16

积分： 36

Re: 研究了下Tslib内关于触摸屏校准的算法，水一贴

优秀！楼主可以再讲讲 tslib 里面的各种滤波器么？在线等.

粗略看了下好像中值滤波，iir，消抖，感觉是常规操作啊:D

打老虎

会员

注册时间： 2019-04-03

已发帖子： 16

积分： 36

Re: 研究了下Tslib内关于触摸屏校准的算法，水一贴

@打老虎
晕了，这个是五点触摸检测法吗

:lol其实就是最小二乘法求系数，哈哈哈